EFFECT OF CROSS-SECTIONAL SHAPE

ON FREE-SURFACE CHANNEL INSTABILITY


Victor M. Ponce and Andrea C. Scott


San Diego State University, San Diego, California

ABSTRACT

A study of the effect of cross-sectional shape on free-surface channel hydrodynamic instability is accomplished. At the outset, the rating exponent β, Froude number F, and Vedernikov number V are identified as the controlling variables. A steep, lined channel is specified for the analysis. The selected design discharge is Q = 100 m3/s, with bottom slope S = 0.06 and Manning's n = 0.025, closely resembling the flow conditions of the Huayñajahuira river, in La Paz, Bolivia, where roll waves have been shown to recur with disturbing regularity. The testing program considers the variation of the bottom width b in the range 5 ≥ b ≥ 1, at 1-m intervals, and the side slope z in the range 0.25 ≥ z ≥ 0, at 0.05 intervals.

The online calculator onlinechannel15b is used to calculate the relevant hydraulic variables, culminating in the values of rating exponent β, Froude number F, and Vedernikov number V  for each of thirty (30) cases. The results show conclusively that as the channel width b is reduced from 5 to 1 m, and the side slope z reduced from 0.25 to 0, that β, F, and V  are reduced, first gradually, and then sharply as z → 0, with the asympotic value z = 0 corresponding to a rectangular channel. For a given design application, these findings may be used to determine optimal geometric cross-sectional values b and z in order to assure that V < 1 and, therefore, avoid flow hydrodynamic instability and the associated roll waves.

1.  INTRODUCTION

Free-surface instability in open-channel flow is generally manifested by the development of roll waves. These are unsteady flow features associated with steep, lined channels, when the Vedernikov number V is greater than or equal to 1 (V ≥ 1). (Ponce, 2014: Section 11.4). However, it can be shown that the actual development of a roll wave depends primarily on the shape of the cross section, whether it is trapezoidal, rectangular, or triangular. For a given channel cross section, there is a unique relationship between the exponent β of the rating (the discharge Q vs flow area A equilibrium rating), and the ratio V/F, in which F = Froude number (Ponce and Choque Guzmán, 2019).

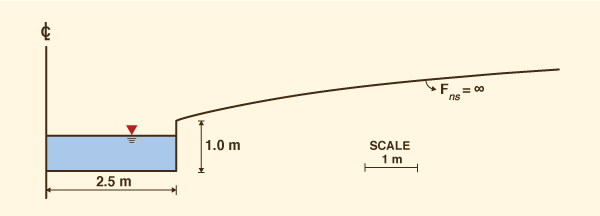
In some circumstances, roll wave phenomena may be of such magnitude as to actually place at risk life and property. This fact is confirmed by the roll waves that occur with worrisome regularity in the Huayñajahuira river, in La Paz, Bolivia, as shown in Fig. 1 and the accompanying video.

[Click on top of photo to watch video]
Courtesy of J. Molina

Fig. 1  Roll wave event on a channelized reach of the Huayñajahuira river,
La Paz, Bolivia, on December 11, 2021.

We posit that the design of a lined channel for the control of roll waves may be accomplished by a judicious choice of cross-sectional shape. The way to accomplish this is to choose, at the design stage, a channel shape that effectively reduces the Vedernikov number below the thresholed value of 1 (V < 1). Therefore, the design focus centers on the value of β, the exponent of the rating, a parameter defined in terms of V/F.

Herein we use the online calculator onlinechannel15b, which determines values of F, V, and β for a prismatic channel (Ponce and Boulomytis, 2021). We run the calculator for a series of cross-sectional shapes, including trapezoidal and rectangular, keeping constant the following variables: (1) discharge Q, (2) Manning's n, and (3) bottom slope S. The effect of the cross-sectional shape is tested by running the calculator for several suitable values of side slope z (z H: 1 V), with the flow depth y set to correspond with the selected discharge Q.

The aim is to examine the behavior and sensitivity of the flow variables to the Froude F and Vedernikov V  numbers, and to the concomitant value of β. In practice, it may be shown that channel stability is attained for values of β close to but clearly greater than 1. Therefore, the optimal cross section, from the standpoint of channel stability, corresponds to the lowest value of β, greater than 1, that is compatible with project cost, optimal footprint dimensions, and other relevant considerations.

2.  BACKGROUND

The theory of hydrodynamic stability of open-channel channel flow is due to Vedernikov (1945). Several years later, Craya clarified the Vedernikov criterion by stating it in terms of the wave celerities (Craya, 1952). The Vedernikov-Craya criterion states that occurrence of roll waves will form when the Seddon celerity equals or exceeds the Lagrange celerity, that is, when the kinematic wave celerity, governed by gravitational and frictional forces, equals or exceeds the dynamic wave celerity, governed by inertial and pressure-gradient forces. In this case, the Vedernikov number exceeds 1: V ≥ 1. Otherwise, V < 1, i.e., dynamic waves travel faster than kinematic waves and, consequently, the flow is stable.

In 1907, Cornish showed, apparently for the first time, a photograph of the fascinating phenomenon in a paper published in the Journal of the Royal Geographical Society (Fig. 2) (Cornish, 1907). In 1948, Powell christened the concept, by stating, to wit: "This criterion, which I am calling the Vedernikov number..." (Powell, 1948). Later, Ven Te Chow referred to the phenomenon as the "Instability of Uniform Flow," implying that under certain conditions, the flow could become unstable and break into a train of roll waves (Chow, 1959: Section 8.8).

Cornish

Fig. 2  Roll waves observed in a canal in the Swiss Alps
at the turn of the 20th century (Cornish, 1907).

The roles of mass and energy are seen to be central to the development of roll waves. While kinematic waves transport mass, dynamic waves transport energy (Lighthill and Whitham, 1955). Therefore, the occurrence of roll waves is seen to be related to the unsteady transport of mass overcoming the unsteady transport of energy. In this light, roll waves are a curious physical manifestation of the preponderance of mass transport over energy transport in unsteady open-channel flow in steep channels (Ponce and Choque Guzmán, 2019).

3.  RELATIONSHIP BETWEEN β AND V/F

There are three characteristic velocities in open-channel hydraulics (Ponce, 1991):

  1. The mean velocity u of the normal, steady flow, expressed by the Manning or Chezy formulas;

  2. The relative velocity v of kinematic waves, expressed by the Seddon celerity formula; and

  3. The relative velocity w of dynamic waves, expressed by the Lagrange celerity formula.

These three velocities can only define two independent, dimensionless ratios, or numbers, to wit: the Froude and Vedernikov numbers (Ponce, 2014: Section 1.3).

The Froude number is the ratio of the velocity of the normal, steady flow u to the relative celerity of dynamic waves w:

             u                u
F  =   ____   =    ________

            w            ( g D )1/2 		(1)

in which D = hydraulic depth (D = A /T ); A = flow area; T = top width; g = gravitational acceleration (Ponce and Choque Guzmán, 2019; Ponce and Boulomytis, 2021).

The Vedernikov number is the ratio of the relative celerity of kinematic waves v to the relative celerity of dynamic waves w:

             v                v
V  =   ____   =    ________

            w            ( g D )1/2 		(2)

The third ratio, a function of the other two, is the dimensionless relative kinematic wave celerity v/u, expressed as follows (Ponce and Choque, 2019):

   v                               V
_____   =   β - 1  =   _____

   u                               F 		(3)

The neutral-stability Froude number Fns is that which corresponds to the Vedernikov number V = 1. Therefore, the neutral-stability Froude number is a function only of β, the exponent of the rating:

                   1
Fns   =     ______

                 β - 1
(4)

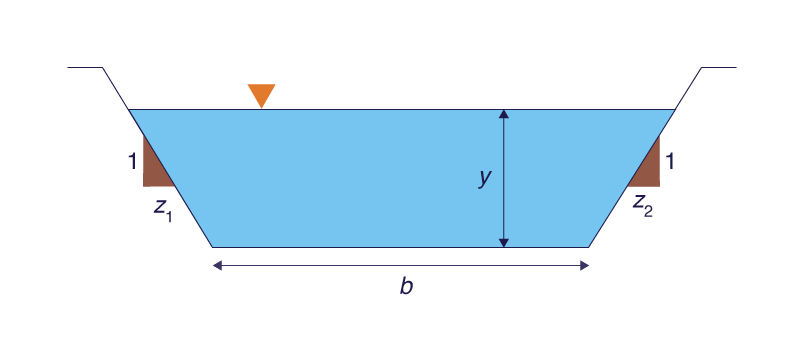
Table 1 shows corresponding values of β and Fns for three asymptotic cross-sectional shapes and two types of friction. The shape of the inherently stable channel has been documented. first by Liggett (1975), and later by Ponce and Porras (1995) (Fig. 3).

Table 1.  Values of β and Fns corresponding to
three asymptotic cross-sectional shapes.
Cross-sectional shape Friction β Fns
Hydraulically wide Manning 5/3 3/2
Chezy 3/2 2
Triangular Manning 4/3 3
Chezy 5/4 4
Inherently stable Manning or Chezy 1 ∞


inherently stable channel
Ponce and Porras

Fig. 3  Shape of the inherently stable channel.

Equation 4 shows that as β  ⇒  1, the neutral-stability Froude number Fns  ⇒  ∞. In practice, however, the Froude number is bounded by the demonstrably finite amount of friction, and maximum Froude numbers do not realistically exceed a value in the range 25-30. Therefore, the inherently stable channel must be considered a theoretical construct.

More importantly, however, certain cross-sectional shapes featuring values of β close to but greater than 1 result in an actual increase in the value of the neutral stability Froude number Fns, effectively reducing the probability that the flow will become unstable. This line of reasoning is pursued in this paper: To find the optimal shape of cross section, typically trapezoidal, that will show to be both practical and stable.

4.  TESTING PROGRAM

4.1  Rationale

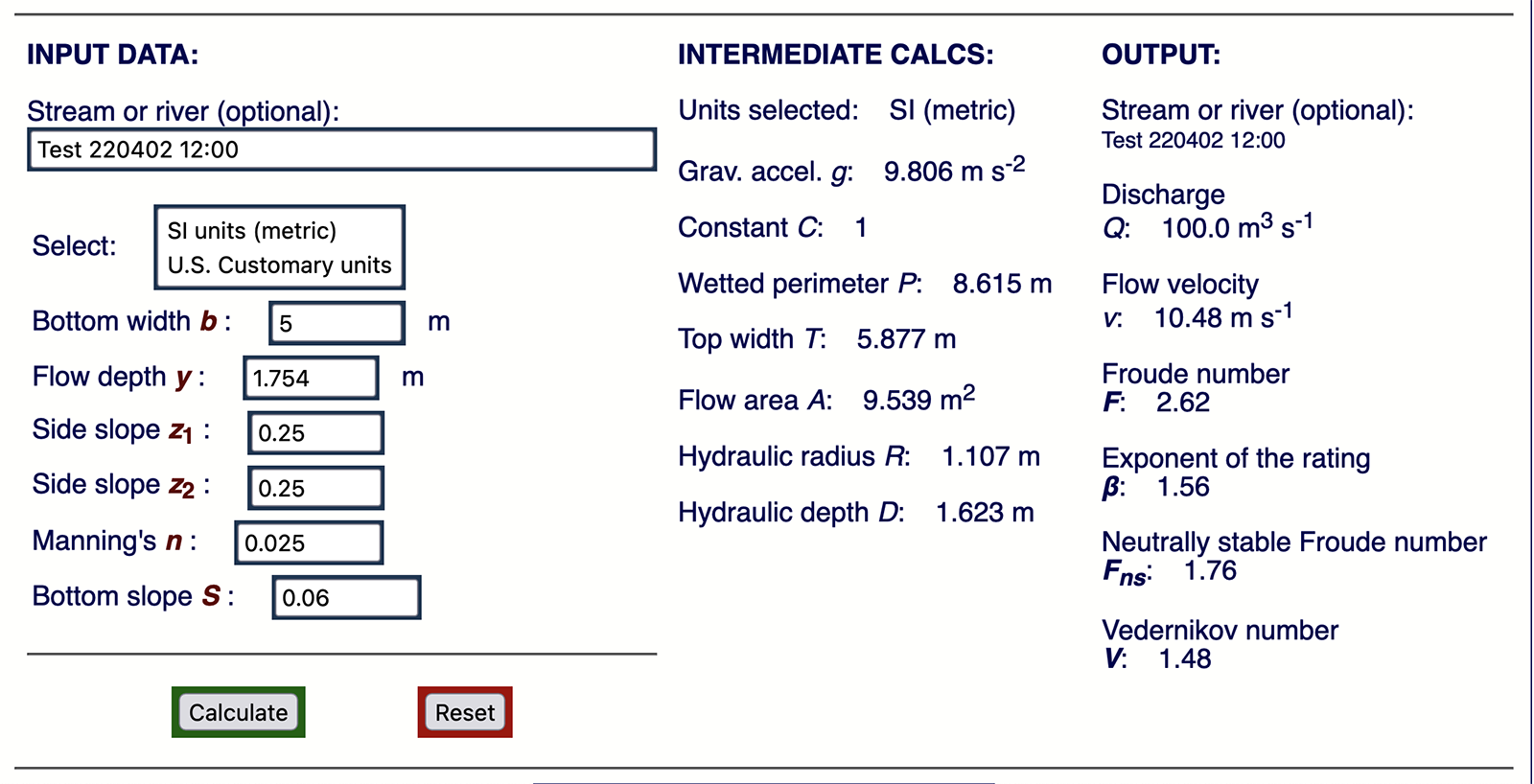
The online calculator onlinechannel15b calculates the value of β, the exponent of the rating, corresponding to a rectangular, trapezoidal, or triangular cross-sectional shape. The calculator requires the following input (Fig. 4):

Input to onlinechannel15b:

  1. Bottom width b

  2. Flow depth y

  3. Side slope z1

  4. Side slope z2

  5. Manning's n

  6. Bottom slope S.


Fig. 4  Definition sketch for a cross section of trapezoidal,
rectangular, or triangular shape.

At the outset, for each design application, determine the applicable values of Manning's n and bottom slope S. The methodology consists of the following steps:

  1. Choose an appropriate value of design discharge Q;

  2. Choose appropriate values of side slopes z1 and z2;

  3. Determine a testing set of values of bottom width b;

  4. Using the online calculator, for each value of bottom width b, calculate, by trial and error, the flow depth y corresponding to the chosen discharge Q; and

  5. Note the output of the online calculator, consisting of the following: (a) [confirming the value of] discharge Q; (b) flow velocity v; (c) Froude number F; (d) exponent of the rating β; (e) neutrally stable Froude number Fns; and (f) Vedernikov number V.

Keeping in mind considerations of flow stability (V < 1) or instability (V ≥ 1), the results are analyzed to choose the optimal design cross-sectional shape compatible with prevailing site and cost constraints.

Fig. 5  Sample calculation for z = 0.25 and b = 5 m, shown in Table 2, Col. 2, using onlinechannel15b.

4.2  Testing program

The testing program is designed to determine the hydraulic conditions in a series of alternative channel cross-sections for which the calculated Vedernikov number varies in the range V ≷ 1. Several values of side slope z are specified, ranging from high (z = 0.25; trapezoidal) to low (z = 0; rectangular), and varying the bottom width b within a suitable range (5 ≥ b ≥ 0). Experience indicates that the chosen range of side slopes (0.25 ≥ z ≥ 0) is likely to provide a desired range of Vedernikov numbers V for appropriate channel flow stability/instability analysis.

The following six (6) side slopes are considered in this study:

  • z = 0.25;

  • z = 0.20;

  • z = 0.15;

  • z = 0.10;

  • z = 0.05; and

  • z = 0.0.

Tables 2 to 7 show the results of the calculation using onlinechannel15b. Generally, when reducing the bottom width b in the chosen range 5 ≥ b ≥ 1, the smaller the value of side slope z, the faster the Vedernikov number V decreases to values less than 1. Indeed. Table 7 shows that the lowest value of V (V = 0.05) is obtained for the case of z = 0 (rectangular channel) and b = 1, i.e., the narrowest value of b within the chosen test range (5 ≥ b ≥ 1). A detailed analysis follows.

Table 2. Results for Series A  (z = 0.25).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.754 2.078 2.581 3.408 4.769
Output flow variables
P 8.615 8.283 8.320 9.025 10.83
T 5.877 5.039 4.290 3.704 3.384
A 9.539 9.391 9.408 9.719 10.45
R 1.107 1.133 1.130 1.076 0.965
D 1.623 1.863 2.192 2.624 3.089
Results
v 10.48 10.65 10.63 10.29 9.569
F 2.62 2.49 2.29 2.02 1.73
β 1.56 1.53 1.48 1.40 1.32
Fns 1.76 1.87 2.07 2.45 3.12
V * 1.48 1.32 1.10 0.82 0.55
* Two stable values of V  were found, shown in bold.

Table 3. Results for Series B  (z = 0.20).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.783 2.128 2.680 3.625 5.260
Output flow variables
P 8.636 8.340 8.466 9.393 11.72
T 5.713 4.851 4.072 3.450 3.104
A 9.55 9.417 9.476 9.878 10.79
R 1.105 1.129 1.119 1.051 0.92
D 1.671 1.941 2.327 2.863 3.477
Results
v 10.47 10.62 10.56 10.13 9.27
F 2.58 2.43 2.21 1.91 1.58
β 1.56 1.53 1.47 1.39 1.30
Fns 1.77 1.88 2.09 2.50 3.26
V * 1.46 1.29 1.05 0.76 0.48
* Two stable values of V  was found, shown in bold.

Table 4. Results for Series C:  (z = 0.15).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.814 2.184 2.795 3.900 5.950
Output flow variables
P 8.668 8.416 8.652 9.887 13.03
T 5.544 4.655 3.838 3.170 2.785
A 9.563 9.451 9.556 10.08 11.26
R 1.103 1.122 1.104 1.019 0.863
D 1.724 2.030 2.489 3.180 4.043
Results
v 10.46 10.58 10.46 9.925 8.888
F 2.54 2.37 2.11 1.77 1.41
β 1.56 1.52 1.47 1.38 1.28
Fns 1.77 1.89 2.11 2.58 3.47
V * 1.43 1.25 0.99 0.68 0.40
* Three stable values of V  were found.

Table 5. Results for Series D:  (z = 0.10).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.849 2.248 2.935 4.269 7.019
Output flow variables
P 8.716 8.518 8.889 10.58 15.10
T 5.369 4.449 3.587 2.853 2.403
A 9.586 9.497 9.666 10.36 11.94
R 1.099 1.114 1.086 0.979 0.790
D 1.785 2.134 2.694 3.630 4.969
Results
v 10.43 10.53 10.35 9.661 8.377
F 2.49 2.30 2.01 1.61 1.20
β 1.56 1.52 1.46 1.37 1.26
Fns 1.77 1.90 2.15 2.68 3.82
V * 1.40 1.20 0.93 0.60 0.31
* Three stable values of V  were found.

Table 6. Results for Series E:  (z = 0.05).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.887 2.322 3.108 4.799 9.037
Output flow variables
P 8.778 8.649 9.223 11.60 19.09
T 5.188 4.232 3.310 2.479 1.903
A 9.613 9.557 9.806 10.74 13.12
R 1.095 1.104 1.063 0.925 0.687
D 1.852 2.258 2.962 4.334 6.892
Results
v 10.40 10.47 10.20 9.307 7.628
F 2.44 2.22 1.89 1.42 0.92
β 1.56 1.52 1.45 1.35 1.22
Fns 1.78 1.91 2.19 2.84 4.52
V * 1.36 1.15 0.86 0.50 0.20
* Three stable values of V  were found.

Table 7. Results for Series F:  (z = 0).
Q = 100 m3/s n = 0.025 S = 0.06
Variable Bottom width b (m)
5 4 3 2 1
Input
y 1.929 2.407 3.330 5.690 16.54
Output flow variables
P 8.858 8.814 9.660 13.38 34.08
T 5.000 4.000 3.000 2.000 1.000
A 9.645 9.628 9.990 11.38 16.54
R 1.088 1.092 1.034 0.850 0.485
D 1.929 2.407 3.330 5.690 16.54
Results
v 10.37 10.39 10.01 8.795 6.050
F 2.38 2.13 1.75 1.17 0.47
β 1.55 1.51 1.44 1.31 1.11
Fns 1.79 1.93 2.24 3.13 8.36
V * 1.33 1.10 0.78 0.37 0.05
* Three stable values of V  were found.

5.  ANALYSIS

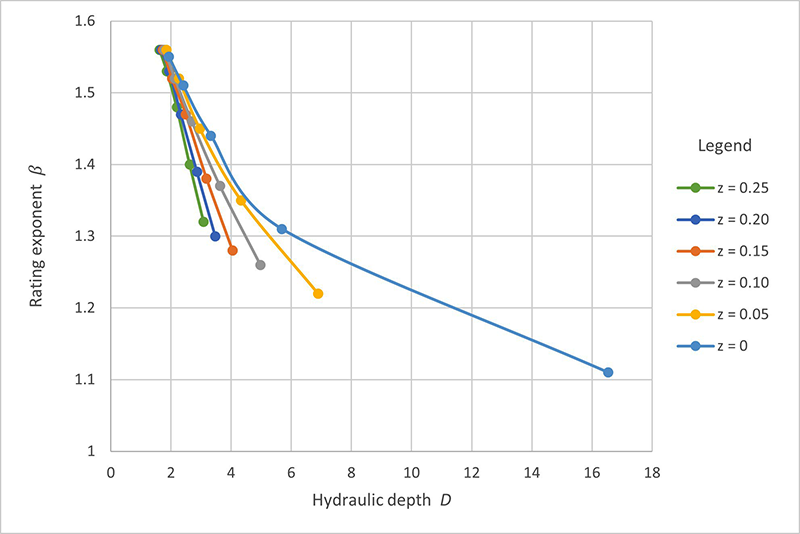
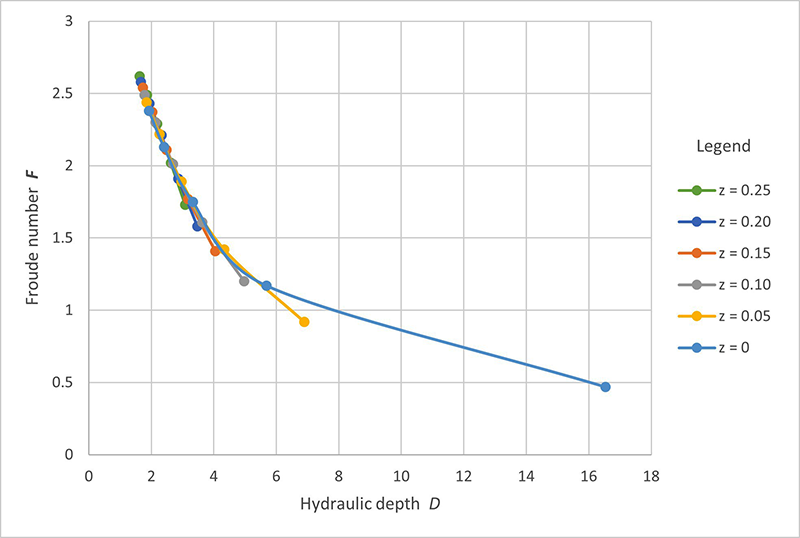
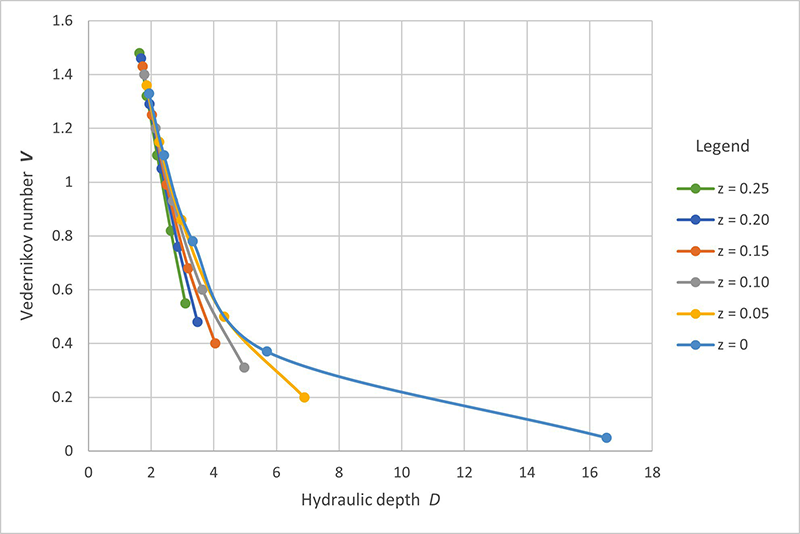
The results of Tables 2 to 7 are analyzed to determine the cross-sectional shape, which in this paper is varied from trapezoidal (z = 0.25; Table 2) to rectangular (z = 0; Table 7), under which the Vedernikov number decreases from the unstable range, V > 1, to the stable range, V ≤ 1. At the outset, it is recognized that the Froude and Vedernikov numbers (Eqs. 1 and 2, respectively) vary inversely with hydraulic depth D. Thus, the larger the value of D, the smaller the values of both Froude and Vedernikov numbers, eventually leading to the condition of stable flow, i.e., V ≤ 1. We pose that herewith is the solution of the stability/instability dichotomy: The larger the hydraulic depth, the more stable is the flow likely to be.

To further explain the findings, the variation, with hydraulic depth D, of the rating exponent β, Froude number F, and Vedernikov number V is shown in Figs. 6 to 8, respectively.

Figure 6 shows that the decrease in β is gradual for the trapezoidal shapes (0.25 ≥ z ≥ 0.05), and sharp (to β = 1.11) for the (asymptotic) rectangular shape (z = 0). Figure 7 shows that the decrease in F is gradual for the trapezoidal shapes (0.25 ≥ z ≥ 0.05), and sharp (to F = 0.47) for the (asymptotic) rectangular shape (z = 0). Figure 8 shows that the decrease in V is gradual for the trapezoidal shapes (0.25 ≥ z ≥ 0.05), and sharp (to V = 0.05) for the (asymptotic) rectangular shape (z = 0).

It is concluded that the fastest way to decrease the Vedernikov number below 1 and, thus, assure hydrodynamic stability, is to choose a bottom width b, in conjunction with a side slope z, that will assure that V < 1.

In practice, a suitable value of V < 1 may be used as a design objective. The results of Tables 2 to 6 indicate that, for the example presented herein, a V = 0.93 is obtained for b = 3 m and z = 0.10. Furthermore, a somewhat lower and, therefore, somewhat more stable V = 0.86 is obtained for b = 3 m and z = 0.05.

The analysis presented here purposely considers only the question of hydrodynamic stability. In an actual design situation, issues such as cost, right-of-way, and constructability may also have a role in determining the optimal cross-sectional shape.

Fig. 6  Rating exponent β  vs. hydraulic depth D.

Fig. 7  Froude number F  vs. hydraulic depth D.

Fig. 8  Vedernikov number V  vs. hydraulic depth D..

6.  CONCLUSIONS

A study of the effect of cross-sectional shape on free-surface channel hydrodynamic instability is accomplished. At the outset, the rating exponent β, Froude number F, and Vedernikov number V are identified as the controlling variables. The rating exponent characterizes the discharge-flow area rating Q = α A β. The Froude number characterizes the flow regime as either: (a) subcritical, (b) critical, or (c) supercritical. The Vedernikov number describes a flow type that is either: (a) stable, (b) neutral, or (c) unstable.

A steep, lined channel is specified for the analysis. The selected design discharge is Q = 100 m3/s, with bottom slope S = 0.06 and Manning's n = 0.025, closely resembling the flow conditions of the Huayñajahuira river, in La Paz, Bolivia, where roll waves have been shown to recur with worrisome regularity. The testing program considers the variation of the bottom width b in the range 5 ≥ b ≥ 1, at 1-m intervals (five channel widths), and the side slope z in the range 0.25 ≥ z ≥ 0, at 0.05 intervals (six side slopes).

The online calculator onlinechannel15b is used to calculate the relevant hydraulic variables, culminating in the values of rating exponent β, Froude number F, and Vedernikov number V  for each of thirty (5 × 6 = 30) cases. The results show conclusively that as the channel width b is reduced from 5 to 1 m, and the side slope z reduced from 0.25 to 0, that β, F, and V  are reduced, first gradually, and then sharply as z → 0, with the asympotic value z = 0 corresponding to a rectangular channel. For a given design application, these findings may be used to determine optimal geometric cross-sectional values b and z in order to assure that V < 1 and, therefore, avoid flow hydrodynamic instability and the associated roll waves.

REFERENCES

Craya, A. 1952. The criterion for the possibility of roll wave formation. Gravity Waves, Circular 521, 141-151, National Institute of Standards and Technology, Gaithersburg, MD.

Cornish, V. 1907. Progressive waves in rivers. Journal of the Royal Geographical Society, Vol. 29, No. 1, January, 23-31.

Liggett, J. A. 1975. Stability. Chapter 6 in Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.

Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.

Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April, 376-380.

Ponce, V. M. 2014. Chow, Froude, and Vedernikov. Proceedings, American Society of Civil Engineers (ASCE) World Environment and Water Resources Congress, June 1-5, 2014, Portland, Oregon.

Ponce, V. M. and B. Choque Guzmán, 2019. The control of roll waves in channelized rivers. http://ponce.sdsu.edu/the_control_of_roll_waves.html   (Cited Aptil 6, 2022).

Ponce, V. M. and V. Boulomytis, 2021. Design of a stable channel on a steep slope using the exponent of the rsting. http://ponce.sdsu.edu/design_of_a_stable_channel_using_the_exponent_of_the_rating.html   (Cited April 6, 2022).

Powell, R. W. 1948. Vedernikov's criterion for ultra-rapid flow. Transactions, American Geophysical Union, Vol. 29, No. 6, 882-886.

Vedernikov, V. V. 1945. Conditions at the front of a translation wave disturbing a steady motion of a real fluid, Dokl. Akad. Nauk SSSR, 48(4), 239-242.

220416 06:00