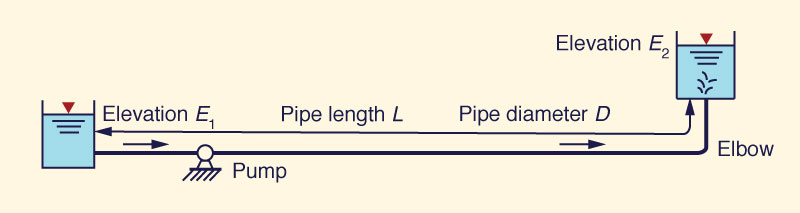
online_pump_pipe_system:  Operating discharge and head in a pump-pipe system
Definition sketch of a pump-pipe system

SAMPLE INPUT     SI units [U.S. Customary units]

  • Pipe diameter D (m) [ft]:  0.5 [1.6404]

  • Pipe length L (m) [ft]:  2000 [6,561.7 ft]

  • Friction factor f =  0.016

  • Upstream reservoir elevation E1 (m) [ft]:  450 [1,476.4]

  • Downstream reservoir elevation E2 (m) [ft]:  500 [1,640.4]

  • Entrance loss coefficient Ke =  0.50

  • Exit loss coefficient KE =  1.00

  • Sum of bend loss coefficient(s) Kb =  0.19 (one bend, r/d = 2)

    Type 1 head-discharge relation:  (Theoretical H-Q head-discharge relation, or pump curve)

    c (m) [ft] :  70 [229.66]

    d (s2/m5) [s2/ft5] :  700 [1.8415]

    Type 2 head-discharge relation:  (Practical H-Q head-discharge array)

    N = 8

    H (i) (m) [ft] :  70, 60, 50, 40, 30, 20, 10, 0  [229.659,196.850,164.042,131.234,98.425,65.617,32.808,0.]

    Q (i) (m3/s) [cfs] :  0., 0.11952, 0.16903, 0.20702, 0.23905, 0.26726, 0.29277, 0.31623  [0.,4.2208,5.9692,7.3108,8.4420,9.4382,10.3391,11.1676]

OUTPUT

    Type 1 head-discharge relation:

  • •  Operating discharge Q (m3/s) [cfs] :  0.1594 [5.6319]

  • •  Operating head H (m) [ft] :  52.2074 [171.2503]

    Type 2 head-discharge relation:

  • •  Operating discharge Q (m3/s) [cfs] :  0.1583 [5.5907]

  • •  Operating head H (m) [ft] :  52.1751 [171.1445]

The minor differences between the two methods are due to the interpolating accuracy in the Type 2 head-discharge relation.

Thank you for running online_pump_pipe_system.   [160610]

Count